Why Do Large Sample Sizes Result In Smaller Standard Errors?

The standard error decreases as the sample size increases due to a fundamental statistical principle. When you have a larger sample size, it allows for a more accurate representation of the entire population. This happens because, as the sample size approaches the true size of the population, the individual sample means become increasingly concentrated around the actual population mean. In other words, when you take a larger sample, you’re more likely to get results that are very close to the true characteristics of the entire population. This reduction in variability leads to a decrease in the standard error, making your estimates more reliable. This statistical phenomenon is crucial for drawing meaningful conclusions from data and is a cornerstone of statistical analysis.

The relationship between sample size and margin of error is inverse, meaning that as the sample size increases, the margin of error decreases. This is due to the fact that with a larger sample size, there is a more comprehensive representation of the population, leading to more accurate and reliable results. In other words, the margin of error is reduced because there is a higher level of confidence in the findings when a larger number of data points are considered. Therefore, increasing the sample size is a crucial factor in reducing sampling error and obtaining more precise conclusions in statistical analysis.

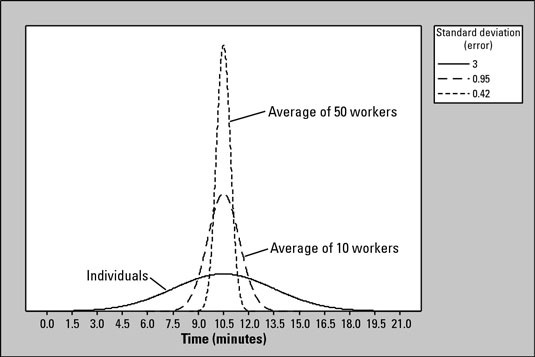
Does the standard error decrease as the sample size increases? The variations in the curves indicate variations in the standard deviation of the sampling distribution. It is observed that smaller sample sizes typically result in larger standard errors, whereas larger sample sizes tend to yield smaller standard errors. To illustrate this point about standard errors in a different manner, consider the following example: